يشكل البرهان شبحا مخيفا بالنسبة للتلاميذ، خاصة في المرحلة الإعدادية حيث يتلقى لأول مرة أنشطة في الرياضيات يتطلب حلها القيام بالبرهنة على صحة متساوية أو تعبير أو علاقة في الرياضيات.
سنتحدث في هذا المقال عن البرهان مركزين أساسا على دروس الرياضيات المبرمجة في المرحلة الإعدادية، على أساس أننا سنتحدث لاحقا في مقال آخر عن البرهان وأنواعه وعلاقته بالمنطق الرياضياتي.
👈ستتعرفون بعد قراءتكم لهذا المقال على ما يلي:
◆ تعريف البرهان بصفة عامة وفي الرياضيات بصفة خاصة
◆ الهدف من البرهان في الرياضيات
◆ مميزات البرهان في الرياضيات
◆ البرهان الرياضياتي بين الابتدائي والإعدادي
◆ مراحل إجراء البرهان في الرياضيات
◆ أمثلة تطبيقية: تطبيقات البرهان في الهندسة
1- ما هو البرهان؟ وما هو البرهان الرياضياتي؟
👈بشكل عام ينطبق مفهوم البرهان على مجموعة متنوعة من التخصصات، حيث يُستعمل كل مرة في نطاق معين مختلف عن النطاق الذي استُخدم فيه مرة سابقة أو لاحقة. ومع ذلك فالتعريف المشترك المتعارف عليه هو أن البرهان في الحقيقة هو التمكن من جمع أدلة أو مبررات أو معايير كافية لإبراز والتأكيد على حقيقة معينة.
👈 في اللغة العربية، للبرهان مرادفات كثيرة منها الدليل أو الحجة أو الإثبات أو التعليل أو التبرير، والهدف منه الوصول إلى نتيجة معينة من أجل الإقناع وعدم الشك.
👈 وقد وردت كلمة "برهان" في القرآن الكريم في عدة مواضع، وتشير بشكل عام إلى الحجة القاطعة، والدليل الواضح، أو البيّنة الصريحة. وتأتي في سياقات مختلفة لتؤكد على حقيقة الرسالة الإلهية، ودعوة الناس إلى الإيمان بالله تعالى.
👈 وفي مجال التواصل (الشفوي أو الكتابي) ومن خلال إجراء المحادثات أو الحوارات أو الخطابات يحاول الناس إقناع بعضهم البعض من خلال القيام بإعطاء أدلة وبراهين لإثبات صحة ما يقولون.
👈 ومن أمثلة البرهان في حياتنا اليومية:
- وجود آثار أقدام في الطريق برهان على أن شخصا ما قد مر من هناك.
- التوفر على شهادة الباكالوريا برهان على النجاح في هذا المستوى.
- رنين المنبه برهان على وصول وقت الاستيقاظ
- وجود ظل برهان على وجود مصدر ضوئي وحاجز.
- وفي الكهرباء، توهج المصباح برهان على مرور التيار في الأسلاك.
- وفي الكمياء، تعكر ماء الجير برهان على وجود غاز ثنائي أوكسيد الكربون
- ...
👈 وغيرها من البراهين التي تعتمد على الحس والتجربة والملاحظة ومن تم البناء عليها، وهذا النوع من البرهان يدعى البرهان التطبيقي ويتبع هذا البرهان كلُّ مسألة تخضع للتجربة والملاحظة مثل علم الكيمياء والطب... وفي المقابل، يوجد البرهان العقلي الذي يعتمد على المنطق والتحليل والتركيب والاستنتاج والربط والاستقراء والتعميم والقياس وهي عمليات فكرية تحصل في الذهن، هي أساس لعملية التفكير والفهم والتدبر، وكل العلوم النظرية التجريدية مثل الرياضيات وفروعها تتبع هذا البرهان.
👈 في الرياضيات، فالبرهان هو طريقة لتعليل أو تبرير صحة عبارة أو علاقة في الرياضيات من خلال الاستناد إلى مجموعة من البديهيات والمسلمات والتعاريف والخصائص والنظريات المثبتة علميا والمتفق عليها مسبقا.
👈 مثال: للبرهنة على توازي مستقيمين نبحث عن الخصائص والتعاريف المثبتة قبليا والمناسبة للوضعية التي نحن بصددها، ومن هذه الخصائص والبديهيات مثلا: إذا كان مستقيان متعامدان فكل مستقيم متعامد على أحدهما يكون موازيا للآخر.
👈 وستتضح الفكرة أكثر في الفقرات الموالية.
👈 وبدون برهان، ستكون النظريات والنتائج اتي نتوصل إليها في الرياضيات مجرد آراء أو تخمينات، وستكون حقيقتها غير مؤكدة. لذلك، يعتبر أداة حاسمة في الرياضيات، وهو الطريقة الأساسية لإثبات صحة البيانات الرياضياتية.
2- الهدف من البرهان في الرياضيات
👈 كما أشرنا في آخر الفقرة السابقة، فإن الرياضيات بدون برهان مجرد كلام فارغ لا معنى لها، ولكي يتم قبول نظرية أو فرضية ما لا بد أن تحصل على برهان منطقي سليم وذلك من خلال المرور طبعا بقواعد الاستدلال بدءا من تلك البديهية (المسلَّم بها والمتعارف عليها والتي لا تحتمل الخطأ) ثم الفرضية وهكذا إلى أن يتم الوصول إلى النتيجة المرجوة.
👈 يتمثل دور البرهان إذن في الرياضيات في:
- التحقق من صحة عبارة ما
- تعليل سبب صحة عبارة ما.
- توصيل معرفة رياضياتية.
- اكتشاف أو بناء معرفة رياضياتية جديدة.
- تنظيم البيانات.
👈كما يمكن القول إن مهمة البرهان الرياضياتي تشبه مهمة المحامي الذي يناقش قضية في قاعة المحكمة، حيث إن مهمته هي إثبات ذنب الشخص أو براءته باستخدام الأدلة والتفكير المنطقي، وبالمثل فإن البرهان في الرياضيات يحاول إظهار صحة عبارة رياضياتية أو نفيها باستخدام التعريفات والنظريات والمسلمات المتفق عليها.
3- خصائص البرهان الرياضياتي
👈 يتميز البرهان في الرياضيات بخصائص تجعله مقبولا ولا يمكن الطعن فيه وهي:
❊الاستنتاج المنطقي: يعتمد البرهان الرياضياتي على سلسلة من الاستنتاجات المنطقية، بدءًا من الحقائق المعروفة أو المفترضة، كالبديهيات أو النظريات المثبتة مسبقًا، وهو يتقدم عبر سلسلة من الخطوات المتلاحقة والمترابطة فيما بينها، حتى يتم الوصول إلى العبارة المطلوب إثباتها.
❊الوضوح والدقة: يكون البرهان الرياضياتي دائمًا واضحًا ودقيقًا، ويجب أن تتم كتابته بطريقة تسهل على مدرس الرياضيات فهمها، دون إدخاله في أي غموض.
❊ الشكلية: يستخدم البرهان الرياضياتي الرموز الرياضياتية للتعبير عن المفاهيم والعلاقات بدقة، حيث تساعد هذه الرموز على إزالة الغموض، وتضمن دقة الاستدلال وأيضا تسهل إجراء البرهان.
❊ الشمولية: يجب أن يغطي البرهان الرياضياتي جميع الحالات ذات الصلة، ولا يجب أن يترك أي شك في صحة العبارة أو المعادلة التي يتم إثباتها.
❊ عدم القابلية للشك: يجب أن يكون البرهان الرياضي مقنعًا بحيث لا يترك مجالًا للشك عند أي شخص عارف بقواعد الرياضيات.
4- البرهان الرياضياتي بين الابتدائي والإعدادي
👈 المبدأ الذي نعتمده في موقعنا دائما هو أننا إذا أردنا تعلم أشاء جديدة في مستوى معين أو في مرحلة معينة، يجب البحث عن موقع هذه الأشياء الجديدة في المستويات أو المراحل السابقة... نظرا لأن المفاهيم الرياضياتية تُكتسب بطريقة التدرج، والسبب الذي يجعل المتعلم غير متمكن أو ضعيف في الرياضيات أو في بعض المفاهيم المتعلقة بها هو تلك التراكمات التي تتراكم عليه من خلال سوء فهمه لما سبق فلا يستطيع بذلك الاستمرار في التعلم إلا بتدارك ما فاته. (يمكن الرجوع إلى مقال حول التدرج بالتعلمات أساس اكتساب الرياضيات)
👈والبرهان الرياضياتي له أيضا نصيب في هذه العملية، فلكي نفهم المقصود من البرهان لابد أن نرجع إلى سنوات التعليم الابتدائي ونبحث عنه هناك، ونتساءل هل البرهان فقط وليد المرحلة الإعدادية أم أنه كان يمارس في الابتدائي؟؟
👈 فدعوني أقول لكم، ولا تتفاجؤوا إن قلت لكم، أن المتعلم يمارس البرهان منذ الابتدائي، لكن طبعا، بشكل ضمني، غير صريح به، وليس بالشكل المعتاد عليه في الإعدادي، وأحيانا أيضا يتم الاكتفاء بالبرهان الشفهي دون الكتابي. وستكتشفون ما أقول لكم من خلال الأمثلة الموالية.
⇚ إذا رجعنا إلى تعريف للبرهان، الذي هو، باختصار، إعطاء أدلة أو مبررات أو معايير كافية لإبراز والتأكيد على حقيقة معينة. فعندما يطلب المدرس في الابتدائي حل مسألة في الرياضيات، هناك من المتعلمين من يجيب، وأحيانا بسرعة، ويعطي الجواب بشكل مباشر، فيسأله المدرس أسئلة مثل: كيف توصلت إلى الجواب؟ ما هي العملية التي استعملتها؟ من أين أتيت بهذا الجواب؟ ... أسئلة مختلفة تثير فضول المتعلم وتجعله في حيرة ويبحث عن تبرير للجواب الذي توصل إليه، ومن هنا بدأ يتعلم المبادئ الأولى للبرهان في الرياضيات.
⇚ بل هناك من المتعلمين من يضع تفصيلا لمجموعة من المراحل عند حل مسألة ما، إلى أن يتوصل إلى الجواب النهائي، كي يتم تبرير ما توصل إليه، فهذا أيضا في حد ذاته برهان.
⇚ وعندما ينجز المتعلم عملية من العمليات الأربع على مختلف أنواع الأعداد (الصحيحة والعشرية والكسرية)، يقارن النتيجة التي توصل إليها مع ما توصل إليه الآخرون، وعندما لا تنطبقان يحاول تبرير صحة أو عدم صحة العمليات من خلال تحديد الخطأ المرتكب بالاعتماد على مكتسباته في إنجاز العمليات... فهذا أيضا برهان.
⇚ كما أنه كثيرا ما نجد أسئلة في الرياضيات مثل: علل جوابك، كيف تفسر ذلك، لماذا...؟ الهدف منها هو إعطاء دليل لتبرير الحل الذي قدمه المتعلم حتى يتمكن المدرس من مدى فهمه للخطة أو الدرس أو المفهوم... فهذا أيضا برهان.
👈هذه نماذج لأمثلة وهناك أخرى كثيرة تبين أن البرهان حاضر أيضا في الرياضيات منذ سنوات الابتدائي لكن، كما أشرنا إلى ذلك، بطريقة ضمنية وغير مباشرة وأحيانا يتم الاكتفاء به شفهيا.
👈 فلا يمكن إذن اعتبار الانتقال من المرحلة الابتدائية إلى المرحلة الإعدادية انكسارا بين المرحلتين، بل يجب أن يكون متصلا و مستمرا من حيث بناء المعارف و استيعاب المفاهيم الجديدة، وذلك تبعا لاستمرارية و سيرورة البناء السيكولوجي للعمليات المنطقية لدى التلميذ. و بالتالي يجب ربط هاتين المرحلتين بجسر متصل و على مراحل تدريجية، تبدأ بإثارة فضول و انتباه التلاميذ و تشجيعهم على التفسير و النقاش من خلال أشكال و أنشطة متنوعة و برفع العوائق النفسية التي غالبا ما تعيق قدراتهم الاستدلالية و تؤدي بهم الى النفور، وجعلهم من خلال أشكال مناسبة و متنوعة يشكون في الأحكام التي يصدرونها عند تعاملهم مع مختلف المسائل في الرياضيات.
👈 وعند الانتقال إلى المرحلة الإعدادية، ويتعامل المتعلم مع الحروف والرموز إلى جانب الأعداد في الرياضيات،( راجع مقال من الحساب العددي نحو الحساب الحرفي ) يأخذ البرهان منحى آخر، ويتم بطريقة أخرى جديدة متبعا لمراحل منهجية منضبطة غير عشوائية ومستعملا مصطلحات جديدة مثل: لدينا، إذن، ومنه، وبما أن ، إذا وفقط ، إذا ..فإن،... ليتوصل في الأخير إلى النتيجة المرجوة التي يريد إثباتها.
👈 ومن بين أنواع الأسئلة التي تطرح في الرياضيات والتي من الضروري الإجابة عنها مستعملا أدلة وبراهين مقنعة:
بين أن ...، أثبت أن ...، علل أن ...، برهن على أن ...، لماذا ...؟ وضح أن ...، فسر لماذا...؟ قارن ...، بسط...، وغيرها من الأسئلة التي تهدف إلى تقييم قدرات المتعلم ومهاراته في التعامل مع المسلمات الرياضياتية والربط بينها للتوصل ولإعطاء نتيجة مقنعة خالية من الشك والغموض. ولكي تكون كذلك لابد من اكتساب قوانين ومراحل إجراء البرهان بعيدا عن الارتجالية والعشوائية.
5- مراحل إجراء البرهان في الرياضيات
👈 كثيرا ما يعتقد المتعلم أنه قد أجاب فعلا عن سؤال في الرياضيات، لكنه في الأخير يتفاجأ بحصوله على نقطة غير مرغوبة أو أن جوابه كان خاطئا (ويقع ذلك كثيرا في الامتحانات أو الفروض)، والسبب في ذلك أن المتعلم إما أنه لم يحترم ترابط التعابير وتسلسل الأفكار أثناء إنجاز البرهان أو أنه لم ينطلق من خاصية أو تعريف لمفهوم رياضياتي متعلق بالضبط بما يريد إثباته أو أنه فقط يتخبط بشكل عشوائي حتى يحصل على النتيجة المطلوب إثباتها فيعتقد أن البرهان صحيح، وهناك طبعا من لم يستطع نهائيا إنجاز البرهان، ويرجع ذلك كله إلى الأسباب التالية:
◀ غياب الفهم الصحيح لمفهوم البرهان بصفة عامة وفي الرياضيات خاصة، ولتجاوز هذا المشكل يجب الانطلاق من مفهوم البرهان في الحياة اليومية للمتعلم قبل الانتقال به إلى الرياضيات، وهذا ما قمنا به في بداية هذا المقال.
◀ الجهل بالمغزى من هذا البرهان والهدف منه ولماذا تتم دراسته في المدرسة. وهذا مشكل عام، أي غير متعلق بالبرهان فقط وإنما بالرياضيات كلها إذ هناك من يسأل عن المغزى من الرياضيات بشكل عام... ولتجاوز هذا المشكل يجب تربية المتعلم منذ بداية تعلمه على الدور الذي تلعبه الرياضيات في حياة الإنسان من خلال ربط التعلمات بواقعه المعاش، وهذا ما نؤكد عليه دائما من خلال المقالات التي ننشرها على موقعنا.
◀ الخلط بين المسلمات والخصائص المعروفة والمثبتة مسبقا وبين ما يجب إثباته والبرهنة عليه، وأيضا الجهل بما يجب الانطلاق منه لإثبات تعبير أو علاقة في الرياضيات خاصة إذا تعددت الخاصيات والمفاهيم الرياضياتية داخل درس واحد أو بعد عدة دروس.
◀ اعتبار بعض العلاقات مسلمات ويتم الانطلاق منها رغم أنها ليست كذلك، كاعتبار مثلا الشكل الهندسي دليلا ويتم الانطلاق منه لإثبات توازي مستقيمين فتراه يكتب مثلا: نستنتج من خلال هذا الشكل أن المستقيمين متوازيين. وهذا خطأ كبير يقع فيه الكثير من المتعلمين، خاصة في مجال الهندسة، حيث يعتمدون على الملاحظة المباشرة.
◀ عدم احترام المراحل الواجب اتباعها لإجراء البرهان حتى يكون مقنعا وخاليا من الغموض ولا يترك مجالا للشك.
ويكمن اختصار هذه المراحل في أربع وهي ما يلي:
❊المرحلة الأولى: القراءة الجيدة للمطلوب إثباته وتفحصه بدقة وإمعان من أجل استخراج المعطيات الصريحة والضمنية التي تساعد على إجراء البرهان.
❊ المرحلة الثانية: البحث عن الخصائص والتعاريف التي لها علاقة بالمطلوب إثباته، من خلال الرجوع بالذاكرة إلى الدرس أو الدروس التي لها علاقة بالموضوع
❊المرحلة الثالثة: صياغة التبريرات بتوظيف لمصطلحات مثل: لدينا... إذن ... ومنه... مع الانطلاق من الخاصيات والتعاريف والربط بينها وبين المعطيات المتوفرة للوصول إلى النتيجة المرجوة.
❊ المرحلة الأخيرة: مرحلة التحق، والتي تأتي للتأكد:
- أولا من حسن اختيار الخصائص والتعاريف المناسبة
- وثانيا من تسلسل الأفكار وترابطه وعدم وجود ما يجعلها منافية لقواعد الرياضيات
- وثالثا من ملاءمة النتيجة مع ما تم الانطلاق منه.
كما يمكن أحيانا توظيف أمثلة للتأكد من صحة ما تم إنجازه.
👈ولعل أصعب مرحلة من بين المراحل السابقة هي المرحلة الثانية، أي عند البحث عن الخصائص والتعاريف التي يجب الانطلاق منها لاستنتاج نتائج جديدة حتى يتم التوصل إلى ما يجب إثباته، خاصة إذا كانت المسألة معقدة وتحتاج إلى تطبيق لكثير من الخاصيات أو التعارف، وللتقليل من صعوبة هذه المرحلة نقترح ما يلي:
◀ فهم الخصائص والتعاريف فهما صحيحا وذلك من خلال فهم العلاقة بين الشرط والنتيجة كما في المثال الموالي، وتطبيق هذه الخصائص أو التعاريف بشكل مباشر على مختلف التمارين المرتبطة بها، قبل تطبيقها العام على مختلف الأنشطة الأخرى:
وأيضا التمييز بين الخاصيات المباشرة والخاصيات العكسية كما هو الشأن بالنسبة لمبرهنة فيتاغورس المباشرة والعكسية.
◀ عدم الاستسلام عندما لم يتم التوصل إلى الجواب، بل يجب إعادة المحاولة بتجربة خاصية أخرى أو تعريف آخر.
◀ التدريب المكثف على البرهان وتنويع الطرق إن كان ذلك ممكنا حتى يستوعب المتعلم طرق القيام به ويدرك أن الحل يمكن التوصل إليه بطريقة أو بأخرى.
◀ التدرج من السهل إلى الصعب والبدء بالأنشطة والتمارين التي تتطلب توظيف أقل من الخاصيات والتعاريف والمسلمات للانطلاق منها، يعني أنه لا يجب أن نطلب من المتعلم في بداية تعلمه للبرهان، إثبات علاقة في الرياضيات يتطلب ذلك توظيف أكثر من خاصية واحدة.
◀ تنبيه المتعلم إلى أن البرهان ليس إلا تطبيق لإحدى الخاصيات أو التعاريف المدروسة على معطيات جديدة.
◀ تسهيل العمل على المتعلم من خلال إعداده للوائح أو مذكرة خاصة يدون فيها كل الخصائص المدروسة والتي لها علاقة بموضوع مشترك، ولتوضيح الفكرة أكثر نقترح عليكم الاستمرار في قراءة الفقرة الموالية.
6- أمثلة تطبيقية: تطبيقات البرهان في الهندسة
👈تسهيلا لإجراء البرهان في الهندسة، نقترح عليكم هنا بعض الخصائص والتعاريف التي يمكن الانطلاق منها حسب نوعية السؤال المطروح وهذه الخصائص تم تقسيمها أيضا حسب المستوى الدراسي في المرحلة الإعدادية الذي تمت برمجتها فيه.
ستكتشفون أن بعض الأسئلة تتكرر في كل مستوى لكن البرهنة عليها يختلف من مستوى إلى أخر أو يتطور من مستوى أدنى إلى مستوى أعلى حسب نوعية التعاريف والخصائص المرتبطة بهذا السؤال والمدروسة في هذا المستوى.
أولا: البرهنة على استقامية نقط معينة وكأمثلة لطبيعة الأسئلة المطروحة:
- بين أن النقط A و B و C مستقيمية
- بين أن النقط A و B و C على استقامية واحدة.
- هل النقط A و B وC تنتمي إلى نفس المستقيم؟ علل جوابك.
- ادرس استقامية النقط ....
- ما طبيعة النقط A و B وC ، علل جوابك
- برهن على أن المستقيم (AB) يمر عبر النقطة C (أو عبر النقطتين C و D )
- بين أن النقطة C تنتمي إلى المستقيم (AB)
👈هذه الأسئلة كلها تحمل نفس المعنى وهو إثبات استقامية النقط، ويختلف هذا البرهان أو الإثبات حسب المستوى الدراسي وحسب الدرس المتعلق به.
✥ في المستوى الأولى إعدادي:
👈 يمكن البرهنة على استقامية النقط من خلال:
◀ الانطلاق من التعريف الخاص بالنقط المستقيمية.
◀ الانطلاق من الزاوية المستقيمة التي يساوي قياسها 180°.
◀ الانطلاق من منتصف قطعة.
◀ الانطلاق من حساب المسافات.
◀ الانطلاق من تطابق مستقيمين:
✥ في المستوى الثالثة إعدادي:
👈 يمكن البرهنة على استقامية النقط من خلال:
◀ الانطلاق من خصائص المتجهات.
◀ الانطلاق من خصائص التماثل المحوري أو المركزي أو الإزاحة
◀ الانطلاق من معادلة مستقيم
◀ الانطلاق من إحداثيات النقط
ثانيا: البرهنة على توازي مستقيمين، وكأمثلة لطبيعة الأسئلة المطروحة:
- بين أن المستقيمين .... متوازيان
- ما طبيعة المستقيمين ...؟ علل جوابك.
- أثبت أن: (D) // (L)
- تحقق من توازي المستقيمين ...
👈 أيضا نفس السؤال يمكن أن نجده في جميع المستويات، لكن للبرهنة عليه ننطلق من الخاصيات أو التعاريف المدروسة:
✥ في المستوى الأولى إعدادي، يمكن البرهنة على توازي مستقيمين:
◀ انطلاقا من خصائص التوازي والتعامد، وهي كالآتي:
◀ انطلاقا من خصائص متوازي الأضلاع:
◀ انطلاقا من خصائص الزوايا التي يحددها مستقيمان مع قاطع لهما وهي كالآتي:
✥ في المستوى الثانية إعداد، يمكن البرهنة على توازي مستقيمين، إضافة إلى ما سبق، من خلال الانطلاق من:
◀ خاصية من خصائص المثلث، وهي:
✥ وفي المستوى الثالثة إعدادي، يمكن البرهنة على توازي مستقيمين من خلال:
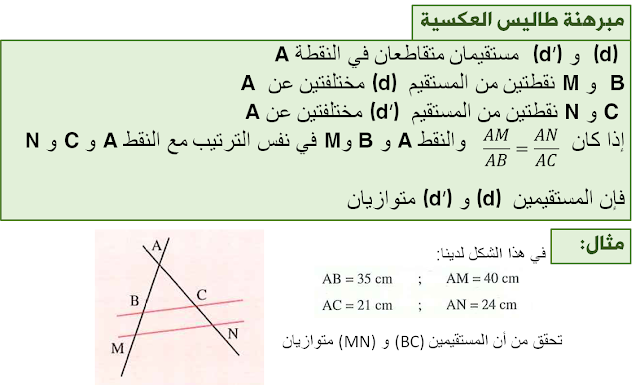
◀ تطبيق مبرهنة طاليس العكسية:
◀ الانطلاق من خصائص المتجهات.
◀ الانطلاق من خصائص الإزاحة.
◀ الانطلاق من معادلة المستقيم
ثالثا: البرهنة على تعامد مستقيمين، وكأمثلة لطبيعة الأسئلة المطروحة:
- بين أن المستقيمين ... متعامدين
- برهن على أن: (AB)┴(CD)
- ما طبيعة المستقيمين ...؟ علل جوابك.
- تحقق من تعامد المستقيمين ...
👈 أيضا نفس السؤال يمكن أن نجده في جميع المستويات، لكن للبرهنة عليه ننطلق من الخاصيات أو التعاريف المدروسة:
✥ في المستوى الأولى إعدادي، يمكن البرهنة على تعامد مستقيمين:
◀ انطلاقا من تعريف التعامد.
◀ انطلاقا من خصائص التوازي والتعامد، وهي كالآتي:
◀ انطلاقا من خصائص المعين أو المربع أو المستطيل.
◀ انطلاقا من تعريف الارتفاع في المثلث.
◀ انطلاق من تعريف مماس الدائرة.
✥ في المستوى الثالثة إعدادي، يمكن البرهنة على تعامد مستقيمين إضافة إلى ما سبق، من خلال:
◀ تطبيق مبرهنة فيتاغورس العكسية:
◀ الانطلاق من معادلة المستقيم
رابعا: البرهنة على منتصف قطعة
👈 للبرهنة على منتصف قطعة يمكن الانطلاق من الخصائص التالية:
1- إذا كانت A وB وI نقط مستقيمية و IA = IB فإن: النقطة I منتصف القطعة [AB].
2- إذا كانت النقطة B مماثلة النقطة A بالنسبة لنقطة I فإن النقطة I منتصف القطعة [AB].
3- إذا كانت I نقطة تقاطع قطري متوازي الأضلاع ABCD فإن: I منتصف [AC] و [BD].
4- إذا كانت I مركز الدائرة (C) التي قطرها [AB] فإن النقطة I منتصف القطعة [AB].
5- إذا كانت I تقاطع واسط القطعة [AB] و المستقيم (AB) فإن I منتصف القطعة [AB].
6- في مثلث ABC، إذا كانت I منتصف [AB]، والنقطة J من المستقيم (AC)، والمستقيم (IJ) يوازي المستقيم (BC) فإن النقطة J منتصف القطعة [AC].
7- خصائص المتجهات وهي:
8- إحداثيات منتصف القطعة.
خامسا: البرهنة على تقايس قطعتين
👈 للبرهنة على تقايس قطعتين يمكن أيضا الانطلاق من عدة خصائص، منها:
1- إذا كانت M تنتمي إلى واسط القطعة [AB] فإن: MA = MB.
2- مماثلة قطعة بتماثل مركزي هي قطعة تقايسها.
3- إذا كان ABC مثلث متساوي الساقين في A فإن: AB = AC.
4- انطلاقا من خصائص المستطيل والمربع والمعين ومتوازي الأضلاع وهي:
• بالنسبة للمربع والمعين، جميع أضلاعه متقايسة
• بالنسبة للمستطيل ومتوازي الأضلاع، كل ضلعين متقابلين متقايسين
• بالنسبة للمستطيل والمربع، القطران متقايسان
5- إذا كانت A و B تنتميان لنفس الدائرة التي مركزها O، فإن: OA = OB.
6- إذا كان المثلث ABC قائم الزاوية في النقطة A، و I منتصف الوتر [BC]. فإن : IA = IB = IC
7- إذا كان مثلثان متقايسين فإن أضلاعهما متناظرة متقايسة.
سادسا: البرهنة على متوازي الأضلاع
👈 للبرهنة على أن رباعيا متوازي أضلاع ننطلق من عدة خصائص، منها:
1- إذا كانت كل ضلعان متقابلان في رباعي حاملاهما متوازيان، فإن هذا الرباعي متوازي الأضلاع.
2- إذا التقى قطرا رباعي في منتصفيهما فإن هذا الرباعي متوازي الأضلاع.
3- إذا كانت كل زاويتين متتاليتين في رباعي متكاملتين فإن هذا الرباعي متوازي الأضلاع.
4- إذا كانت كل زاويتين متقابلتين في رباعي متقايستين فإن هذ الرباعي متوازي الأضلاع.
5- انطلاقا من خصائص المتجهات، وهي:
خلاصة:
👈 تلكم أهم النقط المتعلقة بالبرهان في الرياضيات، وخلاصة القول، للتمكن من البرهان بشكل جيد:
- التكثيف من إنجاز التمارين
- تذكر مختلف الخصائص والتعاريف المدروسة ومحاولة الإتيان بالمناسب منها حسب معطيات التمرين
- عدم الاستسلام عندما لم يتم التوصل إلى الجواب، وإعادة المحاولة بتجربة خاصية أخرى أو تعريف آخر.
- اجتناب التخبط والعشوائية دون دليل مقنع.
- احترام تسلسل الأفكار والتعابير.
- طلب مساعدة من الأستاذ أو من أي شخص آخر موثوق أو من وسائل الاتصال الحديثة.
👈 وإلى هنا نأتي إلى نهاية هذا المقال، نتمنى أن يعجبكم ونتمنى أن تستفيدوا منه، وإن كان كذلك، فلا تنسوا الدعاء لنا ولوالدينا بالرحمة والغفران ولجميع أموات المسلمين، كما لا تنسوا أن تقوموا بنشر محتوى هذا المقال عبر مختلف الوسائل الاتصال حتى تعم الفائدة والسلام عليكم.
المصادر:
- موقع https://reiadyat.com/
- موقع http://ad2math.com/
- موقع https://samerislamboli.com/
- بحث تربوي بعنوان: صعوبة تعلم البرهان الرياضي لدى تلاميذ المستوى الإعدادي في الهندسة من إعداد الأستاذ المتدرب مراد الحجيلي، السنة التكوينية 2013.2014


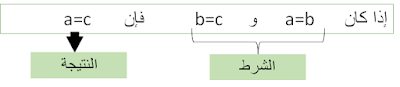



























المرجو عدم نشر تعليقات غير مناسبة للمحتوى